MOVIMIENTO DE ROTACION
Se dice que un sólido rígido está animado de un movimiento de rotación alrededor de un eje fijo cuando todos sus puntos describen trayectorias circulares centradas sobre dicho eje y contenidas en planos normales a éste.
El eje de rotación puede atravesar el cuerpo o ser exterior al mismo; en el primer caso, los puntos del sólido que están sobre el eje permanecen en reposo en tanto que los demás puntos describen circunferencias en torno al eje; en el segundo caso, todos los puntos del sólido están en movimiento circular alrededor del eje exterior al sólido. En cualquier caso, la velocidad v de un punto P del sólido será tangente a la circunferencia descrita y, en un instante dado, tendrá un módulo tanto mayor cuanto mayor sea la distancia del punto al eje de rotación. Dicha velocidad viene dada por
(1)
siendo  un vector unitario (de módulo igual a la unidad) tangente a la trayectoria y v el módulo de la velocidad. Téngase en cuenta que necesariamente
un vector unitario (de módulo igual a la unidad) tangente a la trayectoria y v el módulo de la velocidad. Téngase en cuenta que necesariamente  cambiará a lo largo del movimiento, ya que irá continuamente modificando su dirección hasta llegar de nuevo a la orientación original, tras completar un giro de
cambiará a lo largo del movimiento, ya que irá continuamente modificando su dirección hasta llegar de nuevo a la orientación original, tras completar un giro de  radianes.
radianes.
 un vector unitario (de módulo igual a la unidad) tangente a la trayectoria y v el módulo de la velocidad. Téngase en cuenta que necesariamente
un vector unitario (de módulo igual a la unidad) tangente a la trayectoria y v el módulo de la velocidad. Téngase en cuenta que necesariamente  cambiará a lo largo del movimiento, ya que irá continuamente modificando su dirección hasta llegar de nuevo a la orientación original, tras completar un giro de
cambiará a lo largo del movimiento, ya que irá continuamente modificando su dirección hasta llegar de nuevo a la orientación original, tras completar un giro de  radianes.
radianes.
El módulo de la velocidad, denominado celeridad, se corresponde con
(2)
considerando s la distancia que el sólido va recorriendo a lo largo de la circunferencia. Dada la definición matemática de ángulo  , se verifica que ds = rdθ, para lo cuál habrá que expresar el ángulo en radianes (rad). De aquí se deduce que
, se verifica que ds = rdθ, para lo cuál habrá que expresar el ángulo en radianes (rad). De aquí se deduce que
 , se verifica que ds = rdθ, para lo cuál habrá que expresar el ángulo en radianes (rad). De aquí se deduce que
, se verifica que ds = rdθ, para lo cuál habrá que expresar el ángulo en radianes (rad). De aquí se deduce que(3)
El cociente dθ/dt recibe el nombre de celeridad angular y se designa por ω:
(4)
y podemos expresar la celeridad v de cualquier punto del sólido como el producto de la celeridad angular por la distancia r del punto al eje de rotación
(5)
La introducción del concepto de celeridad angular es de gran importancia por la simplificación que supone en la descripción del movimiento de rotación del sólido, ya que, en un instante dado, todos los puntos del sólido poseen la misma celeridad angular, en tanto que a cada uno de ellos le corresponde una celeridad que es función de su distancia al eje de rotación. Así pues, la celeridad angular caracteriza al movimiento de rotación del sólido rígido en torno a un eje fijo. La celeridad angular se mide en radianes por segundo (rad/s).

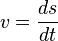




0 comentarios:
Publicar un comentario
Suscribirse a Enviar comentarios [Atom]
<< Inicio